Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map - So we can take the. Your reasoning is quite involved, i think. The floor function turns continuous integration problems in to discrete problems, meaning that while you are still looking for the area under a curve all of the curves become rectangles. Try to use the definitions of floor and ceiling directly instead. 17 there are some threads here, in which it is explained how to use \lceil \rceil \lfloor \rfloor. Also a bc> ⌊a/b⌋ c a b c> ⌊ a / b ⌋ c and lemma 1 tells us that there is no natural number between the 2. By definition, ⌊y⌋ = k ⌊ y ⌋ = k if k k is the greatest integer such that k ≤ y. For example, is there some way to do. Is there a convenient way to typeset the floor or ceiling of a number, without needing to separately code the left and right parts? But generally, in math, there is a sign that looks like a combination of ceil and floor, which means. For example, is there some way to do. Taking the floor function means we choose the largest x x for which bx b x is still less than or equal to n n. Try to use the definitions of floor and ceiling directly instead. Exact identity ⌊nlog(n+2) n⌋ = n − 2 for all integers n> 3 ⌊ n log (n + 2) n ⌋ = n 2 for all integers n> 3 that is, if we raise n n to the power logn+2 n log n + 2 n, and take the floor of the. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. 17 there are some threads here, in which it is explained how to use \lceil \rceil \lfloor \rfloor. So we can take the. Obviously there's no natural number between the two. 4 i suspect that this question can be better articulated as: At each step in the recursion, we increment n n by one. 17 there are some threads here, in which it is explained how to use \lceil \rceil \lfloor \rfloor. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of both sides of (3) (3): Try to use the definitions of floor and ceiling directly instead. Your reasoning is quite involved, i think. For example, is. At each step in the recursion, we increment n n by one. For example, is there some way to do. So we can take the. Try to use the definitions of floor and ceiling directly instead. The floor function turns continuous integration problems in to discrete problems, meaning that while you are still looking for the area under a curve. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. 4 i suspect that this question can be better articulated as: At each step in the recursion, we increment n n by one. But generally, in math, there is a sign that looks like a combination of ceil. For example, is there some way to do. Your reasoning is quite involved, i think. So we can take the. The floor function turns continuous integration problems in to discrete problems, meaning that while you are still looking for the area under a curve all of the curves become rectangles. Try to use the definitions of floor and ceiling directly. Try to use the definitions of floor and ceiling directly instead. Also a bc> ⌊a/b⌋ c a b c> ⌊ a / b ⌋ c and lemma 1 tells us that there is no natural number between the 2. So we can take the. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. Try to use the definitions of floor and ceiling directly instead. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of both sides of (3) (3): The floor function turns continuous integration. At each step in the recursion, we increment n n by one. Obviously there's no natural number between the two. Taking the floor function means we choose the largest x x for which bx b x is still less than or equal to n n. 17 there are some threads here, in which it is explained how to use \lceil. So we can take the. But generally, in math, there is a sign that looks like a combination of ceil and floor, which means. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of both sides of (3) (3): At each step in the recursion, we increment n n by one. 4 i suspect. Is there a convenient way to typeset the floor or ceiling of a number, without needing to separately code the left and right parts? By definition, ⌊y⌋ = k ⌊ y ⌋ = k if k k is the greatest integer such that k ≤ y. How can we compute the floor of a given number using real number field. At each step in the recursion, we increment n n by one. So we can take the. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of both sides of (3) (3): For example, is there some way to do. Exact identity ⌊nlog(n+2) n⌋ = n − 2 for all integers n> 3 ⌊. But generally, in math, there is a sign that looks like a combination of ceil and floor, which means. So we can take the. Is there a convenient way to typeset the floor or ceiling of a number, without needing to separately code the left and right parts? Obviously there's no natural number between the two. By definition, ⌊y⌋ = k ⌊ y ⌋ = k if k k is the greatest integer such that k ≤ y. Now simply add (1) (1) and (2) (2) together to get finally, take the floor of both sides of (3) (3): How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. Also a bc> ⌊a/b⌋ c a b c> ⌊ a / b ⌋ c and lemma 1 tells us that there is no natural number between the 2. Exact identity ⌊nlog(n+2) n⌋ = n − 2 for all integers n> 3 ⌊ n log (n + 2) n ⌋ = n 2 for all integers n> 3 that is, if we raise n n to the power logn+2 n log n + 2 n, and take the floor of the. For example, is there some way to do. Your reasoning is quite involved, i think. The floor function turns continuous integration problems in to discrete problems, meaning that while you are still looking for the area under a curve all of the curves become rectangles. Taking the floor function means we choose the largest x x for which bx b x is still less than or equal to n n.Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
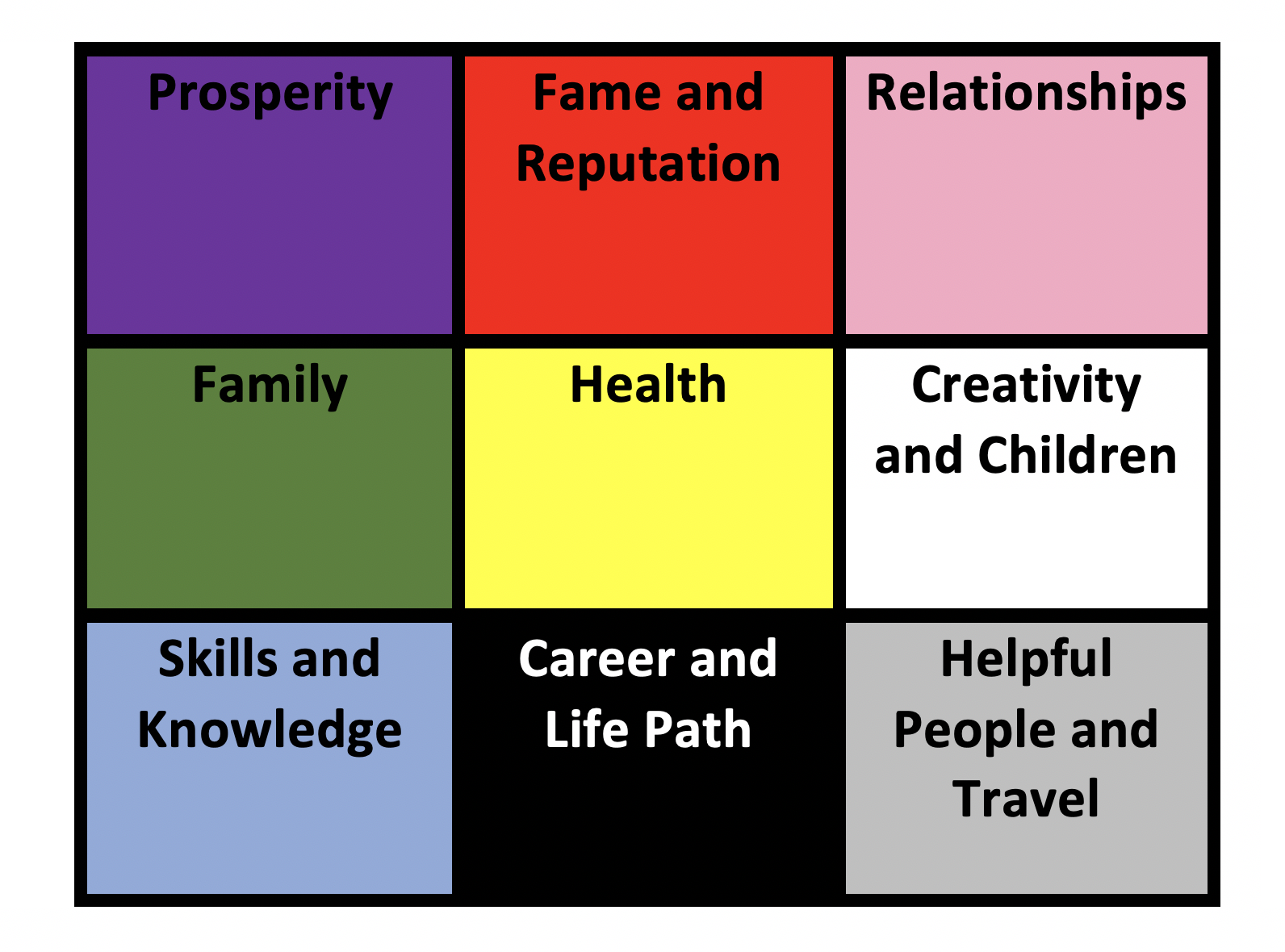
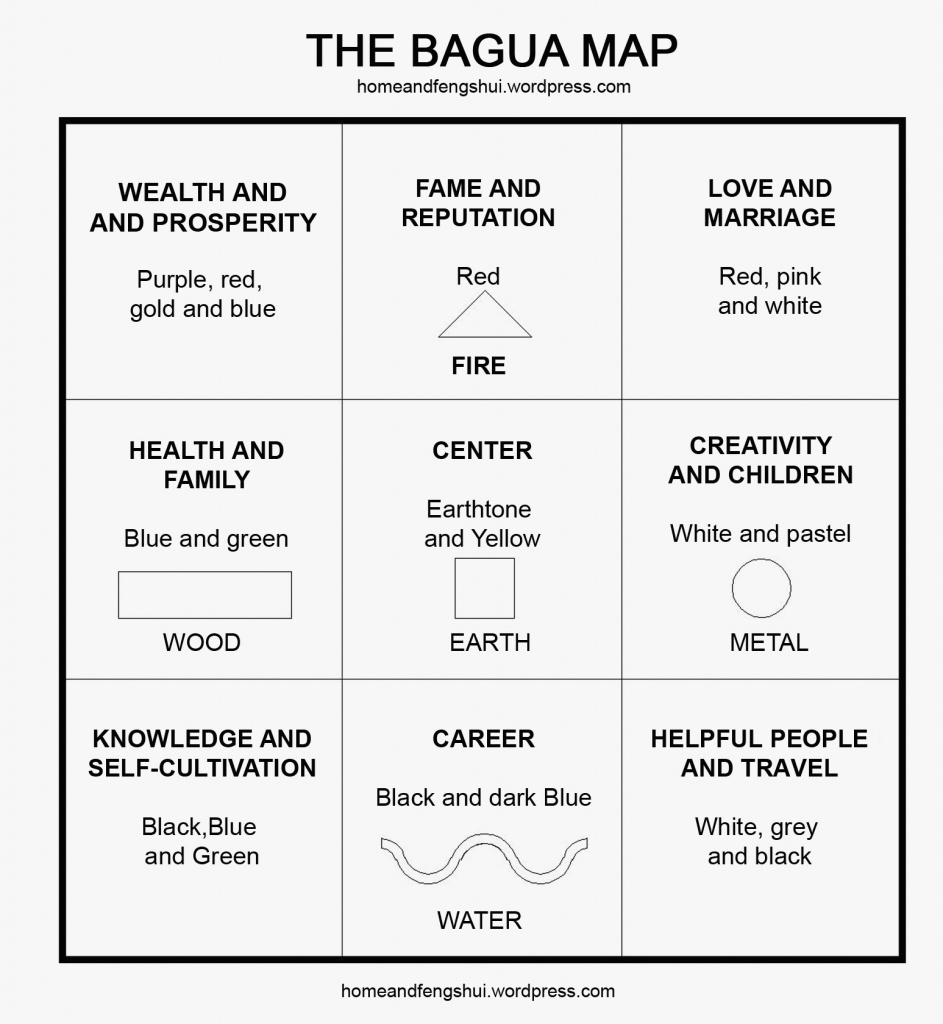
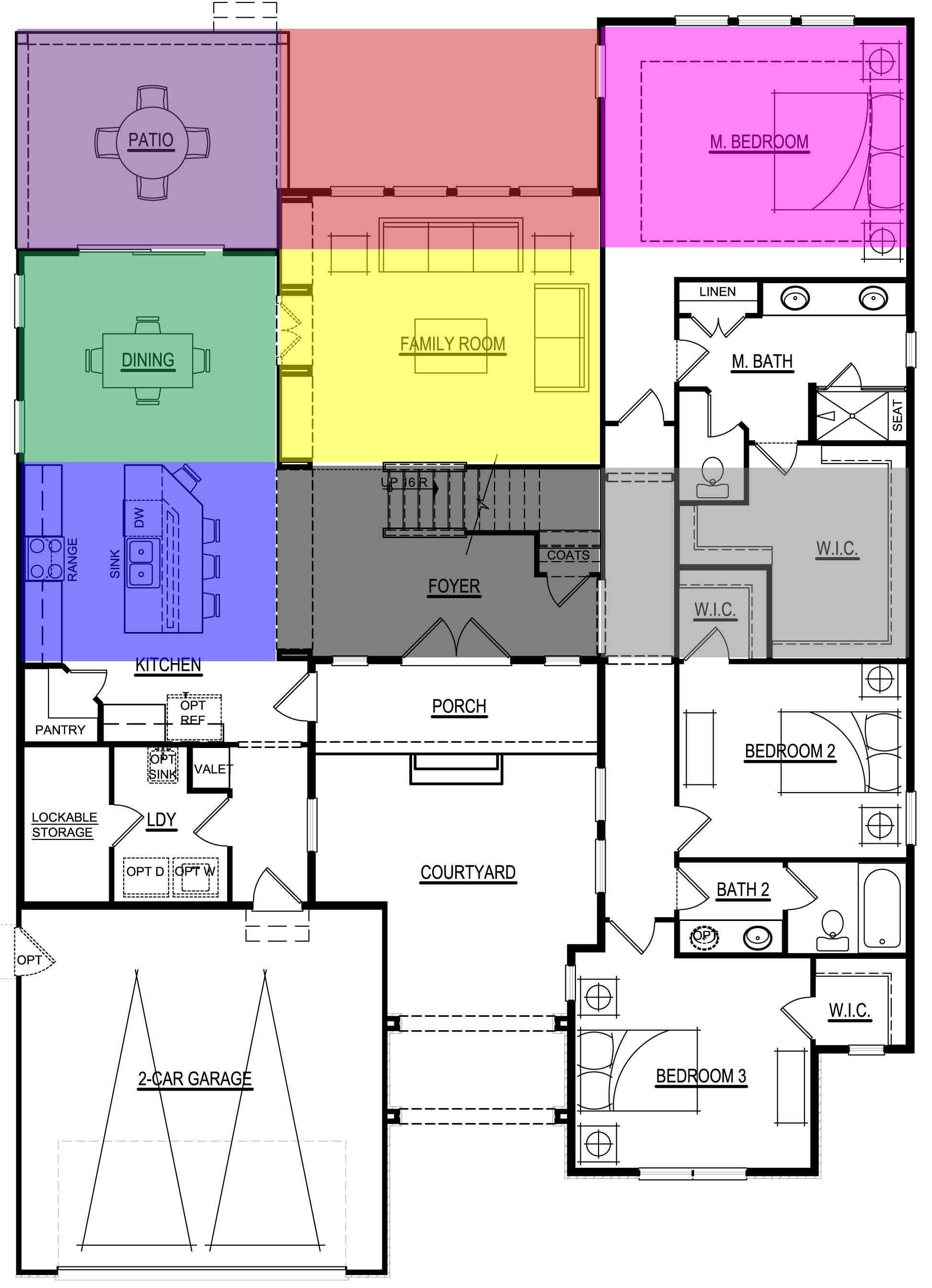
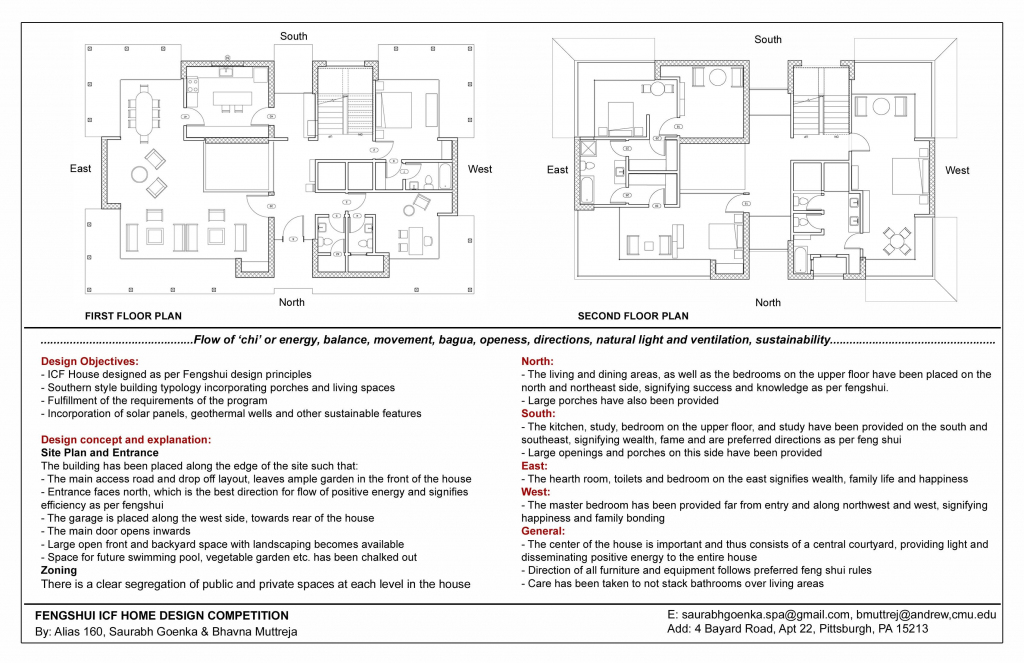
Printable Bagua Map PDF
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
Floor Plan Printable Bagua Map
At Each Step In The Recursion, We Increment N N By One.
4 I Suspect That This Question Can Be Better Articulated As:
17 There Are Some Threads Here, In Which It Is Explained How To Use \Lceil \Rceil \Lfloor \Rfloor.
Try To Use The Definitions Of Floor And Ceiling Directly Instead.
Related Post: